3. Relation to zeros in elastic scattering

It is well known that the soft photon region ( $E_1\approx E_2$) of bremsstrahlung is related to another atomic process - elastic scattering - through the low energy theorem [30]. Consequently the zeros in the soft photon bremsstrahlung matrix elements are related to zeros in elastic scattering. It is possible, for this soft photon region, to write the bremsstrahlung radial matrix element R_l1,l2 in terms of elastic scattering amplitudes or matrix elements. This allows us to see the relationship between zeros in the matrix elements for the two processes.

The relationship between matrix elements can be obtained directly through manipulation of Eq. (10). Here we demonstrate that, as noted, it is a direct consequence of the non-relativistic form of the low energy theorem for soft photons. Low [30] obtained the first two terms of the expansion of the bremsstrahlung matrix element in powers of k, the lowest order term in the series being of order 1/k. If we retain only this lowest order term in Low's expansion and write its non-relativistic form we obtain

$$M^{\rm brem} \rightarrow {1\over k}\hat\epsilon\cdot (\vec p_1-\vec p_2)M^{\rm elas}\quad\mbox{as }k\rightarrow 0,$$ (26)

where $M^{\rm elas}$ is the elastic scattering matrix element. We note that this expression gives a dipole photon angular distribution. That is, we did not make a dipole approximation but, as expected, when we neglect relativistic terms in the low energy theorem (of higher order in the electron velocity $\beta$), we obtain a dipole angular distribution for the emitted photon.

The matrix elements in Eq. (26) correspond to total matrix elements, not radial matrix elements. To obtain the corresponding relationships for the radial matrix elements we must expand $M^{\rm brem}$ and $M^{\rm elas}$ in partial waves series. The expansion of $M^{\rm brem}\equiv M^{\rm nrd}_{fi}$ can be found in Eq. (2) and we simply write down the expansion of $M^{\rm elas}$,

$$\begin{eqnarray*}M^{\rm elas} = {2\over\pi\sqrt E}\sum_{lm} f^{\rm elas}_l(p) Y_{lm}(\hat p_2) Y^*_{lm}(\hat p_1), \end{eqnarray*}$$

where the elastic scattering amplitudes

$$f^{\rm elas}_l(p) = {e^{i(\delta_l+\sigma_l)} \sin(\delta_l+\sigma_l)\over p}.$$ (27)

We write the right hand side of Eq. (26)

$$\begin{eqnarray*}M^{\rm brd}_{fi}\rightarrow{2\over\pi\sqrt E}{1\over k}\sum_m ... ...} f^{\rm elas}_{l'}(p) Y_{l'm'}(\hat p_2) Y^*_{l'm'}(\hat p_1), \end{eqnarray*}$$

where the notation for the spherical vector $(\hat\epsilon)_n$ has been used (see Section 1). Note that we are not retaining terms of higher order in k; we have used $p_1\approx p_2\equiv p$ (for the magnitudes only!). We now utilize the orthogonality properties of the spherical harmonics,

$$\begin{eqnarray*}\int d\Omega\, Y_{lm}(\Omega) Y^*_{l'm'}(\Omega) = \delta_{ll'}\delta_{mm'}, \end{eqnarray*}$$

to select individual partial wave terms on both sides of Eq. (26). We obtain

$$R_{l_1,l_2} = (-1)^{l_1}{4\pi p^3\over k^2}e^{-i(\delta_{l_... ...a_{l_2})}\left[ f^{\rm elas}_{l_1}- f^{\rm elas}_{l_2}\right]$$ (28)

Thus R_l1,l2 can be expressed in terms of the elastic scattering amplitudes for partial waves l₁ and l₂. If we insert the expressions, Eq. (27), for $f^{\rm elas}_l$ in terms of elastic scattering phase shifts we obtain Eq. (10).

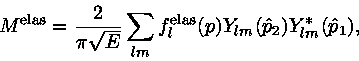
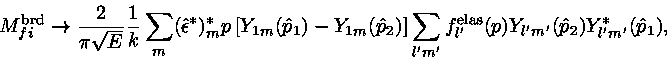
We now discuss some features of the elastic scattering matrix elements that are, in view of the previous discussion, relevant to zeros in the bremsstrahlung matrix element. It is well known from the theory of elastic scattering that, in a short range potential at very low energy, the l=0 phase shift and therefore the l=0 matrix element dominates [6]. Under circumstances described in [31] it is possible that the l=0 phase shift can pass through $n\pi$, n=0, 1, 2, ... in a region where it is the dominant phase shift (the potential must be sufficiently strong at small r to accommodate an integral number of wavelengths of the l=0wavefunction at energies where other phase shifts are small). This causes a zero in the dominant l=0 matrix element in elastic scattering and therefore a minimum in the total elastic scattering matrix element $M^{\rm elas}$. Such minima are called ``Ramsauer-Townsend minima''. They have been observed in experiments involving elastic scattering from noble gas atoms [31]. In Figure 7.3 we show the phase shifts obtained by Holtsmark [13] using a Hartree-Fock potential with an imposed long-range static dipole interaction resulting from static polarizability (see [32]). We see that at energies less than about 5 eV, the l=0 phase shift is dominant, while near 2 eV it passes through $3\pi$, causing a Ramsauer-Townsend minimum. It is also clear from this figure that (modulo $\pi$) the same phase shifts, and thus the elastic scattering amplitudes, cross near 2 eV, causing a zero and sign change in the soft photon bremsstrahlung matrix element in Eq. (28). We refer back to Figure 7.1 which, if we take E⁰=2 eV, represents the soft photon result for Argon. In that figure we have sketched a possible trajectory of zeros, passing through this soft photon zero. From our discussion we can be assured that in cases where Ramsauer-Townsend minima occur there will also be zeros in the (s-p) bremsstrahlung matrix element away from the soft photon limit.